The race for quantum supremacy has gained quite a momentum lately: research centers around the world (in the United States, Europe and China), large technology corporations (including Google, IBM, Intel and recently — Honeywell), or partnerships like D-Wave are not only taking part, but some of them also began to boldly announce that they had crossed the finish line.
Of course, this is currently typical PR activity and we definitely do not live in a world shown in the great series, Devs. Not yet, anyway. Why?
- The technology hasn’t arrived yet, even though the market has already started shaping. There are some signs that quantum computers are becoming more and more powerful, and they are going to have a tremendous impact on our lives 20 years from now.
- Quantum computers are not faster than standard computers. They, in fact, will be much slower. But they will be better thinkers/mathematicians. This means that, for example, they should be able to solve some specific and very complex exponential mathematical equations in seconds instead of millions of years (time required for standard supercomputers). Does it look impossible? They are slower, but also way faster? I will try to explain this in a further part of this text.
- In the near future, quantum computers may contribute to the speed with which humanity’s responses to pandemics are determined and deployed.
The way they work is in line with Nature, which is also quantum.
What we can be sure of is that in the world of quantum computers a lot is happening at the level of public relations: companies announce the achievement of quantum supremacy, or, for example, announce they ARE GOING TO have their working quantum computers ready soon.
In October 2019, Google boasted that their 53-qubit quantum computer solved the mathematical problem of random number generation in 3 minutes and 20 seconds. According to Google, the same task undertaken by the currently fastest IBM supercomputer (Summit) would take 10,000 years. Of course, Google’s PR announced back then that the company has attained quantum supremacy (defined as the moment that a quantum computer performs a calculation impossible for any conventional computer).
But IBM’s PR quickly rebutted this claim, arguing that the Google quantum computer test was not entirely reliable and was based on incorrect assumptions. According to IBM, with the right parameters, this work would be done by the Summit supercomputer in less than 72 hours.
In March 2020, Honeywell announced:
…a breakthrough in quantum computing that accelerates the capability of quantum computers and will enable the company to release the world’s most powerful quantum computer within the next three months.
…we’ll see.
At the same time, other tech giants, such as Accenture, Alibaba Group or Amazon, are taking their seats at the quantum computing table with software development kits, superfast algorithms, cloud solutions and other services.
Yes, quantum computers will be available primarily in the cloud. They will not be crammed into our smart watches, smartphones, laptops etc. — these devices are still destined to be equipped with standard electronic processors, which are significantly more flexible and universal. As cloud computing is everywhere, everybody will be able to easily access Quantum Computing power through online services.
As you can see, the situation in this field is dynamic and each of the big players wants to achieve the so-called quantum supremacy. Time will show who will be first to get the prize of a significant technological advantage in the field of quantum operations. But why did this race start at all? What is it about quantum computers that makes tech giants so determined to develop this technology?
What is a “normal computer”?
In a standard digital computer, data is processed in the form of bits, i.e. 1s (ones) and 0s (zeros). On the technological level, the desired logic state is obtained by properly controlling transistors (allowing current flow or blocking it). Transistors are used to build logic gates (OR, AND, XOR, NOR, etc.), which form entire complex systems of currently manufactured processors that can fit billions of transistors on an area of a few square centimeters.
Over the more than seven decades of digital computer development, miniaturization has progressed significantly. Suffice it to say that currently we carry in our pockets computers with information processing power and reliability many times greater than the first “computer” (the 30 tons ENIAC from 1943).
Quantum computer explained
For a quantum computer, the situation is a little different. The data is stored in so-called qubits (or “quantum bits”).
In the simplest terms, the qubit can, with a certain probability, be in state 1, as well as, with some probability, in state 0.
Also, it can remain in both states simultaneously (and, in fact, in an infinite number of states between 0 and 1) until the measurement is made.
The measurement changes the state of the qubit, which then acquires a certain value. This effect of being in many states at the same time causes the majority of problems in understanding its operation. One researcher described the situation saying that the qubit is undecided before being measured. It is only when the measurement is made that it feels urged to make an immediate decision.
What happens in a qubit is the basic principle of quantum physics called superposition. Quantum superposition occurs when two or more different physical processes are carried out simultaneously. For example, if the electron is to travel from A to B, it will go along an infinite number of trajectories at once. All of them, not only the straight line, as we could imagine based on our intuition. We can say that during the movement “its state is in the superposition of various positions”. Until the electron is observed by anyone on the way, it behaves exactly as if it were in many places at once. But if we decide to measure its location, it will show up (decide) in one randomly selected location.
This, of course, is only an approximation of subatomic particle behavior. To explain a qubit’s features let’s try to find one card among four cards dealt using a standard computer and a quantum machine.
Example

We have 4 cards (ace, king, queen and jack). We shuffle the cards and spread them out on the table face down.
A standard computer
Approaching the task in the standard way, the situation can be described by 4 tests, where 1 means the position in the distribution with the location of the queen card. As given in the table, individual tests can be saved in 4 memory cells.
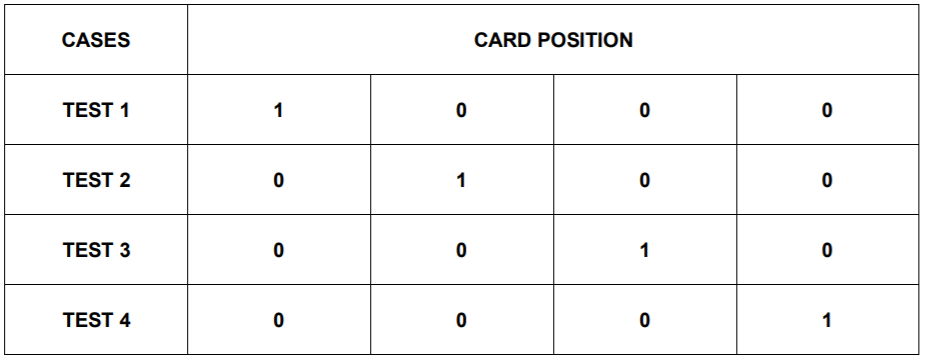
Tests can be saved in 4 memory cells.
In our simple case, we can write a program that will perform tests 1–4 one after another. Test 1 — we turn over the first card (i.e. we check the first memory cell). If we did not find the queen, then we go to test 2 and reveal the second card. We continue to do so until we find the queen. With a sufficiently large number of repetitions of the program launch and different card layouts (location of the lady) statistically, we should be able to discover the queen on average every 2.5 checks performed by the program.
What does the situation look like with a quantum computer?
The problem presented can be described in 2 qubits, so that using the superposition properties, we can perform 4 operations at the same time. The queen card — like the electron — is in a superposition until we measure its location.
The general formula for the number of states in superposition is
2 ^ N, where in our case N = 2.
This means that we will find the required card …in one step.
Moreover!
We always get the result in the first step. To clarify: this depends on the quantum algorithm that has to be prepared and later used. Quantum computing always has a relation to probability and quantum noises (explained later), which means that we have to repeat the tests several times to be sure that the probability is high enough to make an informed decision. But even with this limitation, when the number of solution states grows to the levels that supercomputers should spend billions of years to calculate, quantum computers could have a solution in minutes or hours. They are not faster, they just work differently.
Not just faster
The example given above shows that quantum computers are not just faster versions of digital computers. What they will bring is a fundamental change in the approach to problem solving. The more possible states appear, the greater the benefits we will get from using a quantum computer.
In terms of machine speed, they are billions of times slower than standard computers. But at the same time, they can perform certain math tasks trillions of times faster.
Currently, the fastest supercomputer in the world is the already-mentioned IBM Summit. It’s a real monster with over 2.4 million processors, 250 petabytes of memory (it is estimated that the human brain’s ability to store memories is equivalent to about 2.5 petabytes of binary data) and energy consumption comparable to that of a small town. And it cost about $ 200 million.
This incredible machine can (theoretically) generate the computing power of 200PFLOPS and covers the area of about two tennis courts.
200 PFLOPS is A LOT.
To quote the Knowledge Base of the Indiana University to grasp the scale:
A 1 petaFLOPS (PFLOPS) computer system is capable of performing one quadrillion (1015) floating-point operations per second. The rate 1 PFLOPS is equivalent to 1,000 TFLOPS (1,000 000 GFLOPS). To match what a 1 PFLOPS computer system can do in just one second, you’d have to perform one calculation every second for 31,688,765 years.
According to asteroidsathome.net you would have to combine several Intel(R) Core(TM) i7 processors to reach about 5 GFLOPS performance.
Let’s assume that our goal is to build a computer with twice the power of Summit.
It is relatively simple: build the same supercomputer and connect the two to get double the performance (let’s skip the complicated technological aspects of such a procedure). As a result of this action, we have a 400PFLOPS computer that cost us $400 million. We can increase the computer’s power freely. Each doubling requires doubling the equipment.
This is described by a simple formula: N + N = 2N.
A computer with 8 times more power?
You’re welcome: 8 supercomputers; cost: approximately 1.6 billion dollars (8 times $200 million).
Scaling is different for a quantum computer. Due to the already discussed quantum superposition, doubling the power requires adding another cubit.
So a 3-qubit computer has a power 2 times greater than a 2-qubit. A 4-qubit computer has a power 2 times greater than a 3-qubit. It can be seen that the increase in efficiency at the exponential rate of 2 ^ N.
It must be remembered that each additional qubit is of microscopic size. Since the increase in power for quantum computers is so dynamic (with the increase in qubit numbers), one may consider using a quantum computer for, say, breaking popular RSA asymmetric keys (private and public keys).
I am planning to write my next post exactly about that, so if you are interested, feel invited and come back in a few weeks’ time.
COVID-19
The computational power of quantum computers is just round the next corner. Much of the information on this subject is part of the PR game of the largest players, and therefore should be approached with caution. However, in the context of this powerful computing power, it is impossible not to think about committing it to fighting the COVID-19 epidemic. Is the technology mature enough to help humanity?
It looks like it is. One of the recent examples is D-Waves announcing recently that they provide Free Quantum Cloud Access for Global Response to COVID-19.
Because the most important thing in the fight against the epidemic is the vaccine, the question arises whether quantum computers can accelerate the work on its creation.
The answer is: yes.
Quantum computers could conduct, analyze and prepare an impact assessment for thousands of variables — all of which can be fully connected with one another and which are changing over the time (like virus mutations). Some use cases that can be potentially supported by quantum computers in the near future include:
- the modeling and simulation of the spread of the virus and assessing the rate of virus mutation,
- the assessment of existing drugs as potential treatments.
This is an extremely important aspect. Nowadays, even the most powerful supercomputers cannot analyze all cross-relations between multiple variables. Due to the complexity of the relations, they are able to prepare an impact analysis for a subset of potential paths. This limitation is no longer valid when using quantum computers. Then can easily cover the entire scope.
Would you like more information about this topic?
Complete the form below.